Have you ever come across a noisy image? I mean an image that was not that clear when viewing it? I think we do come across such images very often, especially when many images nowadays are taken by our mobile phone cameras or low-resolution digital cameras.
If you had only that noisy image which means something to you, but the issue is that it cannot be viewed properly, would there be a solution to recover from such noise?
This is where image filtering comes into play, and this is what I will be describing in this tutorial. Let’s get started!
Image Filtering
Image filtering is a popular tool used in image processing. At the end of the day, we use image filtering to remove noise and any undesired features from an image, creating a better and an enhanced version of that image. Two types of filters exist: linear and non-linear. Examples of linear filters are mean and Laplacian filters. Non-linear filters constitute filters like median, minimum, maximum, and Sobel filters.
Each of those filters has a specific purpose, and is designed to either remove noise or improve some aspects in the image. But how is filtering carried out? This is what we will see in the next section.
How Do We Perform Image Filtering?
In order to carry out an image filtering process, we need a filter, also called a mask. This filter is usually a two-dimensional square window, that is a window with equal dimensions (width and height).
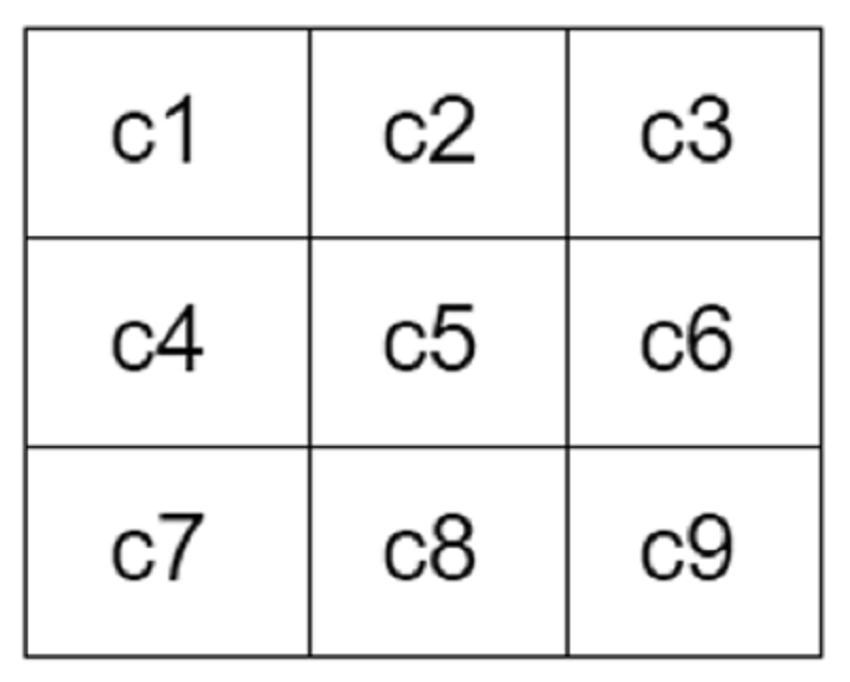
The filter will include numbers. Those numbers are called coefficients, and they are what actually determines the effect of the filter and what the output image will look like. The figure below shows an example of a 3x3 filter, having nine values (coefficients).

To apply the filter, the 3x3 window is slid over the image. This process of sliding a filter window over an image is called convolution in the spatial domain. The window will be placed on each pixel (i.e. think of it as a cell in a matrix) in the image, where the center of the filter should overlap that pixel.
Once this overlap happens, the pixels in the sub-image that the filter is on top of will be multiplied with the corresponding coefficients of the filter. In this case, we will have a new matrix with new values similar to the size of the filter (i.e. 3x3). Finally, the central pixel value will be replaced by a new value using a specific mathematical equation depending on the type of filter used (i.e. median filter).
I know the above paragraph is a bit wordy. Let’s take an example to show how an image filter is applied in action. Suppose we have the following sub-image where our filter overlapped (i and j refer to the pixel location in the sub-image, and I refers to the image):

The convolution of our filter shown in the first figure with the above sub-image will look as shown below, where I_new(i,j) represents the result at location (i,j).
I_new(i,j) = v1 x I(i-1,j-1) + v2 x I(i-1,j) + v3 x I(i-1,j+1) + v4 x I(i,j-1) + v5 x I(i,j) + v6 x I(i,j+1) + v7 x I(i+1,j-1) + v8 x I(i+1,j) + v9 x I(i+1,j+1)
The process is repeated for each pixel in the image, including the pixels at the boundary of the image. But, as you can guess, part of the filter will reside outside the image when placing the filter at the boundary pixels. In this case, we perform padding.
This process simply means that we insert new pixel values in the sub-image under the part of the filter that comes outside of the image before the convolution process, since that part apparently does not contain any pixel values. It is outside of the image! Those padded pixels could be zeros or a constant value. There are other methods for setting the padding values, but these are outside the scope of this tutorial.
I think that’s enough theory for now, so let’s go ahead and get our hands dirty with coding! In this tutorial, I will be explaining the median filter (i.e. non-linear) and the mean filter (i.e. linear) and how we can implement them in Python.
Median Filter
In the median filter, we choose a sliding window that will move across all the image pixels. What we do here is that we collect the pixel values that come under the filter and take the median of those values. The result will be assigned to the center pixel.
Say our 3x3 filter had the following values after placing it on a sub-image:

Let’s see how to calculate the median. The median, in its essence, is the middle number of a sorted list of numbers. Thus, to find the median for the above filter, we simply sort the numbers from lowest to highest, and the middle of those numbers will be our median value. Sorting the values in our 3x3 window will give us the following:
17 29 43 57 59 63 65 84 98
To find the middle number (median), we simply count the number of values we have, add 1 to that number, and divide by 2. This will give us the location of the middle value in the window, which is our median value. So the median value will be at location 9+1/2 = 5, which is 59. This value will be the new value of the pixel under the center of our 3x3 window.
This type of filter is used for removing noise, and works best with images suffering from salt and pepper noise. The image below shows an example of a picture suffering from such noise:

Now, let’s write a Python script that will apply the median filter to the above image. For this example, we will be using the OpenCV library. Kindly check Install OpenCV-Python in Windows and Install OpenCV 3.0 and Python 2.7+ on Ubuntu to install OpenCV.
To apply the median filter, we simply use OpenCV’s cv2.medianBlur() function. Our script can thus look as follows:
import cv2
import argparse
# create the argument parser and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument('-i', '--image', required = True, help = 'Path to the input image')
args = vars(ap.parse_args())
# read the image
image = cv2.imread(args['image'])
# apply the 3x3 median filter on the image
processed_image = cv2.medianBlur(image, 3)
# display image
cv2.imshow('Median Filter Processing', processed_image)
# save image to disk
cv2.imwrite('processed_image.png', processed_image)
# pause the execution of the script until a key on the keyboard is pressed
cv2.waitKey(0)
Notice that I have used argparse, as it is a good practice to be flexible here, and use the command-line to pass the image we want to apply the median filter on as an argument to our program.
After passing our image as a command-line argument, we read that image using the cv2.imread() function. We then apply the median filter using the medianBlur() function, passing our image and filter size as parameters. The image is displayed using the cv2.imshow() function, and is saved to the disk using cv2.imwrite().
The result of the above script is as follows:

Well, what do you think? Very beautiful—a nice and clean image without noise.
You can download the above code from my median-filter repository on GitHub.
Mean Filter
The mean filter is an example of a linear filter. It basically replaces each pixel in the output image with the mean (average) value of the neighborhood. This has the effect of smoothing the image (reducing the amount of intensity variations between a pixel and the next), removing noise from the image, and brightening the image.
Thus, in mean filtering, each pixel of the image will be replaced with the mean value of its neighbors, including the pixel itself. The 3x3 kernel used for mean filtering is as shown in the figure below, although other kernel sizes could be used (i.e. 5×5):

What the above kernel is actually trying to tell us is that we sum all the elements under the kernel and take the mean (average) of the total.
An important point to mention here is that all the elements of the mean kernel should:
- sum to 1
- be the same
Let’s take an example to make things more clear. Say we have the following sub-image:

When applying the mean filter, we would do the following:
(7+9+23+76+91+7+64+90+32)/9 = 44
The exact result is 44.3, but I rounded the result to 44. So the new value for the center pixel is 44 instead of 91.
Now to the coding part. Let’s say we have the following noisy image:

What we want to do at this point is apply the mean filter on the above image and see the effects of applying such a filter.
The code for doing this operation is as follows:
import cv2
import numpy as np
import argparse
# create the argument parser and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument('-i', '--image', required = True, help = 'Path to the input image')
args = vars(ap.parse_args())
# read the image
image = cv2.imread(args['image'])
# apply the 3x3 mean filter on the image
kernel = np.ones((3,3),np.float32)/9
processed_image = cv2.filter2D(image,-1,kernel)
# display image
cv2.imshow('Mean Filter Processing', processed_image)
# save image to disk
cv2.imwrite('processed_image.png', processed_image)
# pause the execution of the script until a key on the keyboard is pressed
cv2.waitKey(0)
Notice from the code that we have used a 3x3 kernel for our mean filter. We have also used the filter2D() function to apply the mean filter. The first parameter of this function is our input image, the second is the desired depth of the output image ddepth, and the third parameter is our kernel. Assigning -1 for the ddepth parameter means that the output image will have the same depth as the input image.
After running the code on our noisy image, this was the result I obtained:
.png)
If you observe the output image, we can see that it is smoother than the noisy image. Mission done!
You can download the above code from my mean filter repository on GitHub.
Conclusion
As we have seen in this tutorial, Python allows us to carry out advanced tasks like image filtering, especially through its OpenCV library, in a simple manner.
Additionally, don’t hesitate to see what we have available for sale and for study in the marketplace, and don’t hesitate to ask any questions and provide your valuable feedback using the feed below.